distribution function for box of particles split in half 8.4.1 One-particle distribution functions. What is the mean number of particles in the box of volume d 3 r A about r A? The probability that particle 1 is in d 3 r A about r A is Many laptop bodies are made of the element aluminium, used for its light weight, strength and appearance. Steel is also a common material for structural support components and hardware .
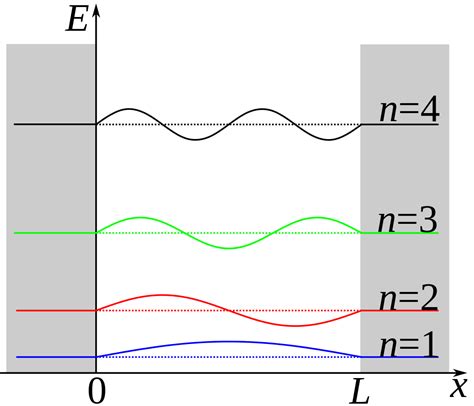
0 · Splitting the wave function of a particle in a box
1 · Radial distribution functions — GROMACS 2021
2 · Radial distribution functions — GROMACS 2019.2 documentation
3 · Lecture 24: Radial Distribution Function — Computational
4 · LECTURE 13 Maxwell–Boltzmann, Fermi, and Bose Statistics
5 · How do you find the number of states unlabeled
6 · Extending Radial Distributions
7 · Distribution of particles in states of matter — Advanced
8 · 8.4: Distribution Functions
9 · 8.2: Bose
The basic cost to Remodel an Electrical Box is $1,271 - $1,541 per box in September 2024, but can vary significantly with site conditions and options. Use our free HOMEWYSE CALCULATOR to estimate fair costs for your SPECIFIC .
The radial distribution function (RDF) or pair correlation function \(g_{AB}(r)\) between particles of type \(A\) and \(B\) is defined in the following way:Distribution of particles in states of matter# Additional Readings for the Enthusiast# Frenkel and Smit , 7.1-7.3. Goals for this lecture# Describe where the probability distributions of where particles are in a simulation box. Algorithmically determine the radial distribution function g(r) .Distribution Functions We can formalize this somewhat. We consider a gas of N identical particles in a volume V in equilibrium at the temperature T . We shall use the following notation: Denote the energy of a particle in state r by εr. Denote the number of particles in state r by nr. r or s.
beige house metal roof
8.4.1 One-particle distribution functions. What is the mean number of particles in the box of volume d 3 r A about r A? The probability that particle 1 is in d 3 r A about r A isThe way to allow radial distribution functions to be calculated all the way out until all particles are counted is to calculate the true v_i, which is the intersection volume between the simulation box and the concentric spheres that make up v_i . If we have n particles and 3 boxes, we can take \(n − k\) particles in the first two boxes (with \(n − k + 1\) possible states) and k particles in the third box. But \(k\) can be anything from zero to \(n\), so that the total number of states is \[\sum_{k=0}^{n}(n . This paper addresses the question of what happens to a particle in a box that is initially in the ground state, when the box is split into two slightly unequal halves.
252 is "ten choose 5", the number of ways to choose five particles from 10. Think of the particles as being labeled 1,2,3.10 and think about the ways you can put all of them on the left-hand side. There's one way to do that, of .
The radial distribution function (RDF) or pair correlation function \(g_{AB}(r)\) between particles of type \(A\) and \(B\) is defined in the following way:where \(\langle N(r) \rangle\) is the average number of particles in a shell of radius \(r\) and thickness \(\Delta r\) around a central particle, \(\rho\) is the number density of particles, and \(r\) is the distance from the central particle. The radial distribution function provides information about the local structure of a system, such as the presence of short-range order, long-range .The radial distribution function (RDF) or pair correlation function \(g_{AB}(r)\) between particles of type \(A\) and \(B\) is defined in the following way:
Distribution of particles in states of matter# Additional Readings for the Enthusiast# Frenkel and Smit , 7.1-7.3. Goals for this lecture# Describe where the probability distributions of where particles are in a simulation box. Algorithmically determine the radial distribution function g(r) Understand how g(r) changes for different states of .Distribution Functions We can formalize this somewhat. We consider a gas of N identical particles in a volume V in equilibrium at the temperature T . We shall use the following notation: Denote the energy of a particle in state r by εr. Denote the number of particles in state r by nr. r or s. 8.4.1 One-particle distribution functions. What is the mean number of particles in the box of volume d 3 r A about r A? The probability that particle 1 is in d 3 r A about r A isThe way to allow radial distribution functions to be calculated all the way out until all particles are counted is to calculate the true v_i, which is the intersection volume between the simulation box and the concentric spheres that make up v_i .
If we have n particles and 3 boxes, we can take \(n − k\) particles in the first two boxes (with \(n − k + 1\) possible states) and k particles in the third box. But \(k\) can be anything from zero to \(n\), so that the total number of states is \[\sum_{k=0}^{n}(n-k+1)=\frac{(n+2)(n+1)}{2}=\frac{(n+3-1) !}{n !(3-1) !}\]
This paper addresses the question of what happens to a particle in a box that is initially in the ground state, when the box is split into two slightly unequal halves. 252 is "ten choose 5", the number of ways to choose five particles from 10. Think of the particles as being labeled 1,2,3.10 and think about the ways you can put all of them on the left-hand side. There's one way to do that, of course.The radial distribution function (RDF) or pair correlation function \(g_{AB}(r)\) between particles of type \(A\) and \(B\) is defined in the following way:
where \(\langle N(r) \rangle\) is the average number of particles in a shell of radius \(r\) and thickness \(\Delta r\) around a central particle, \(\rho\) is the number density of particles, and \(r\) is the distance from the central particle. The radial distribution function provides information about the local structure of a system, such as the presence of short-range order, long-range .
The radial distribution function (RDF) or pair correlation function \(g_{AB}(r)\) between particles of type \(A\) and \(B\) is defined in the following way:Distribution of particles in states of matter# Additional Readings for the Enthusiast# Frenkel and Smit , 7.1-7.3. Goals for this lecture# Describe where the probability distributions of where particles are in a simulation box. Algorithmically determine the radial distribution function g(r) Understand how g(r) changes for different states of .
Distribution Functions We can formalize this somewhat. We consider a gas of N identical particles in a volume V in equilibrium at the temperature T . We shall use the following notation: Denote the energy of a particle in state r by εr. Denote the number of particles in state r by nr. r or s. 8.4.1 One-particle distribution functions. What is the mean number of particles in the box of volume d 3 r A about r A? The probability that particle 1 is in d 3 r A about r A isThe way to allow radial distribution functions to be calculated all the way out until all particles are counted is to calculate the true v_i, which is the intersection volume between the simulation box and the concentric spheres that make up v_i . If we have n particles and 3 boxes, we can take \(n − k\) particles in the first two boxes (with \(n − k + 1\) possible states) and k particles in the third box. But \(k\) can be anything from zero to \(n\), so that the total number of states is \[\sum_{k=0}^{n}(n-k+1)=\frac{(n+2)(n+1)}{2}=\frac{(n+3-1) !}{n !(3-1) !}\]
This paper addresses the question of what happens to a particle in a box that is initially in the ground state, when the box is split into two slightly unequal halves. 252 is "ten choose 5", the number of ways to choose five particles from 10. Think of the particles as being labeled 1,2,3.10 and think about the ways you can put all of them on the left-hand side. There's one way to do that, of course.
bel electrical boxes
Splitting the wave function of a particle in a box
beige house what color metal roof
Radial distribution functions — GROMACS 2021
Radial distribution functions — GROMACS 2019.2 documentation
I need help identifying a Kennedy toolbox I came across. It's a 7 drawer toolbox looks like a 520 series but what makes it stick out is that it has brass handles on all of the drawers and an old 3 digit seasmee combination lock on it.
distribution function for box of particles split in half|LECTURE 13 Maxwell–Boltzmann, Fermi, and Bose Statistics